Wie man Sudoku Rätsel löst - Echte Tipps und Ratschläge (Teil 3)

Im letzten Teil dieses Artikels hatten wir 4 von 9 Quadraten eines Sudoku-Rätsels erfolgreich gelöst. Jetzt arbeiten wir weiter, indem wir auf dem aufbauen, was wir wissen. 

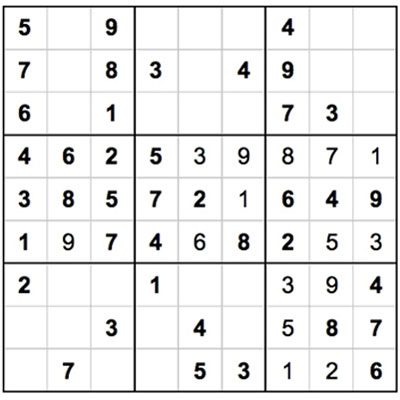
Wenn man Sudokus löst, hilft es, mit der "tief hängenden Frucht" zu beginnen - den Teilen des Puzzles, die bereits viele Zahlen haben. Wenn wir uns die Quadrate, Zeilen und Spalten ansehen, können wir Möglichkeiten finden, alle 9 Zahlen an ihren Platz zu bringen, basierend auf dem, was bereits auf dem Gitter platziert ist. 

In diesem Puzzle hat die dritte Spalte von links 7 von 9 Zahlen platziert. Die einzigen verbleibenden Zahlen sind 4 und 6. Wenn wir zu den benachbarten Feldern hinüberblicken, sehen wir eine 4 und eine 6 im unteren rechten Feld. Jetzt können wir 4 und 6 eliminieren - wir wissen, dass die 4 in die untere rechte Ecke des unteren linken Quadrats und die 6 in die obere rechte Ecke des unteren linken Quadrats gehen muss. 

Wir haben auch genügend Informationen, um eine 1 in das untere linke Quadrat zu setzen - rechts in der Mitte (es gibt eine 1 in der linken Spalte und in der oberen Reihe, die in das untere linke Quadrat läuft - das bedeutet, dass der einzige Platz, den die 1 noch hat, das "Quadrat" in der Mitte des unteren linken Quadrats des Gitters ist). 

Jetzt müssen nur noch die Zahlen 5, 8 und 9 in das untere linke Feld gesetzt werden. Ein einfacher Eliminierungsprozess hilft, diese Zahlen zu platzieren. 

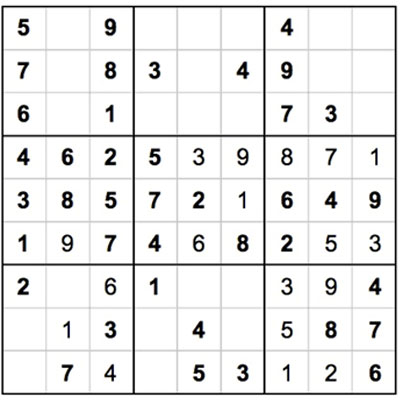
In den unteren beiden Reihen der benachbarten Quadrate gibt es die Zahl 5, so dass wir eine 5 in die obere Reihe (mittlere Spalte) des unteren linken Quadrats setzen können. 

Jetzt sind nur noch die beiden Zahlen 8 und 9 übrig. Wieder können wir den Eliminierungsprozess verwenden - es gibt bereits eine Zahl 8 im unteren rechten Quadrat, mittlere Reihe, mittlere Spalte. Das bedeutet, dass die 8 in der unteren linken Ecke des unteren linken Quadrats platziert werden kann und die einzige verbleibende Zahl, 9, an der letzten verbleibenden Stelle. 

Lose Enden zusammenbinden

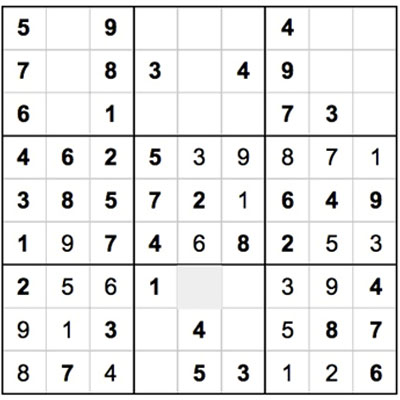
Jedes Mal, wenn wir eine neue Nummer in Sudoku platzieren, "ändert sich das Spiel". Nun, da wir das untere linke Quadrat des Gitters fertiggestellt haben, wie wirkt sich das auf die benachbarten Quadrate aus? Welche anderen Zeilen oder Spalten können wir, basierend auf dem, was wir jetzt wissen, vervollständigen? 

Wenn wir auf das untere mittlere Quadrat, auf die oberste Reihe schauen, sehen wir, dass 7 von 9 Zahlen bereits platziert wurden. Die einzigen fehlenden Zahlen sind 7 und 8. Im mittleren Quadrat des Gitters steht eine 8 in der rechten Spalte - das heißt, wir können eine 7 in die obere rechte Ecke des unteren mittleren Quadrats setzen, und wir können eine 7 in den oberen mittleren Raum dieses Quadrats setzen. 

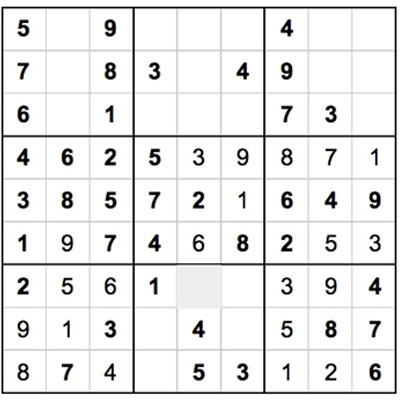
Das untere mittlere Quadrat hat nur noch 3 Zahlen übrig - 2, 6 und 9. Wenn wir auf die benachbarten Quadrate schauen, sehen wir eine Zahl 9 im unteren linken Quadrat, mittlere Reihe - das bedeutet, dass die 9 nur in der unteren linken Ecke des unteren mittleren Quadrats platziert werden kann.

Sackgasse? Probiere es woanders.

Nachdem wir die 9 in das untere mittlere Feld gesetzt haben, sind noch 2 Felder übrig - aber wir können nicht herausfinden, welche Zahlen wir dort platzieren sollen. Wir sind in einer vorübergehenden Sackgasse. Wenn man festsitzt, ist es oft am besten, zu einem ganz anderen Teil des Gitters zu springen. In diesem Fall schauen wir auf das linke obere Quadrat - wo es nur noch 3 Zahlen gibt: 2, 3 und 4. 

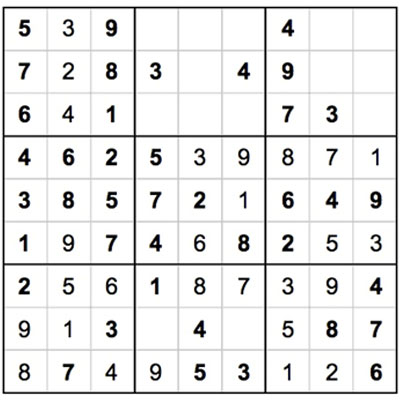
Wir sehen 3 im oberen mittleren Quadrat (mittlere Reihe, linke Spalte) und oberen rechten Quadrat (untere Reihe, mittlere Spalte). Das bedeutet, dass die 3 im oberen linken Feld in die obere Reihe gehen muss. 

Jetzt müssen wir eine 4 und eine 2 platzieren, es gibt bereits eine 4 im oberen mittleren Quadrat (mittlere Reihe, rechte Spalte), so dass wir eine 4 in der unteren Reihe des oberen linken Quadrats und eine 2 in der restlichen Stelle platzieren können. 

Jetzt haben wir 6 von 9 Feldern des Gitters fertiggestellt - dieses Sudoku-Rätsel ist fast gelöst! Unser nächster Artikel wird den Denkprozess zeigen, wie man dieses Gitter fertigstellen kann.